How can I use dynamic programming in Scheme to solve the Coin Change problem?

Question

I'm trying to learn a Lisp language and have settled on Guile and am trying to solve this problem:

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

You may assume that you have an infinite number of each kind of coin.

Fundamentally, I understand the basic of dynamic programming where you can use recursion and memoization in order to save calculating at lower depths, but as Lisp I would expect it to be perfect for this type of problem. The problem I am having is returning separate lists for each combination of coins.

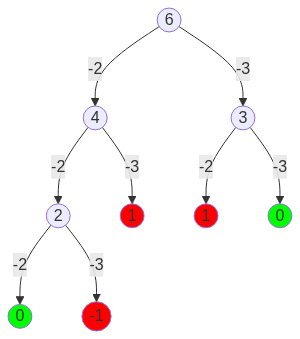
For an example case, consider target of 6 with coins [2, 3]. The simple tree would look like this:

The correct answer would be (3 3) with the other "complete" solution being (2 2 2).

However, if I try and construct these, the form I would want to use (without memoization) would look something like this.

(define get-coins (lambda (coins target) 
    (cond
        ((= target 0) '())
        ; not quite sure how to "terminate" a list here 
        ; An idea is to return (list -1) and then filter 
        ; lists that contain -1
        ((< target 0) ?????) 
        (else
            ; for each coin, recurse
            (map (lambda (v)
                (cons v (get-coins coins (- target v))))))
    )
))

However, this doesn't return more lists as it goes through. Rather, it creates nested lists. And this is my problem. Any help with this would be greatly appreciated.

Answer 1

I wanted to avoid nested lists, so I used a variable results:

(define (get-coins coins target)
  (let ((results '()))

Then I defined the function get-coins-helper, similar to your get-coins. And whenever I found some possible result, I used set! to update results:

 (letrec ((get-coins-helper
              (lambda (coins target result)
                (cond ((= target 0) (set! results (cons result results)))
                      ((< target 0) '())
                      (else (map (lambda (value)
                                   (get-coins-helper coins
                                                     (- target value)
                                                     (cons value result)))
                                 coins))))))

Then I called (get-coins-helper coins target '()) to find all possible results and at the end, I checked the value of results and returned -1 (if results are empty) or the shortest element of results:

      (if (null? results)
          -1
          (car (sort results (lambda (x y) (< (length x)
                                              (length y))))))

Full code:

(define (get-coins coins target)
  (let ((results '()))
    (letrec ((get-coins-helper
              (lambda (coins target result)
                (cond ((= target 0) (set! results (cons result results)))
                      ((< target 0) '())
                      (else (map (lambda (value)
                                   (get-coins-helper coins
                                                     (- target value)
                                                     (cons value result)))
                                 coins))))))
      (get-coins-helper coins target '())
      (if (null? results)
          -1
          (car (sort results (lambda (x y) (< (length x)
                                              (length y)))))))))

Some tests:

> (get-coins '(2 3) 6)
'(3 3)
> (get-coins '(2 3) 1)
-1

Answer 2

Using fold to choose best solutions. The result is a list whose car is the number of coins and cdr is the list of chosen coins. In the event that no solutions are feasible, (+inf.0) is returned.

(use-modules (srfi srfi-1))

(define (get-coins coins target)
  (fold (lambda (coin best)
          (let [(target (- target coin))]
            
            (cond [(zero? target)
                   (list 1 coin)]
                  
                  [(positive? target)
                   (let* [(res (get-coins coins target))
                          (score' (1+ (car res)))]
                     (if (< score' (car best))
                         (cons score' (cons coin (cdr res)))
                         best))]
                  
                  [(negative? target)
                   best])))
        (list +inf.0)
        coins))

(get-coins (list 2) 6)
$8 = (3 2 2 2)

(get-coins (list 2 3) 6)
$9 = (2 3 3)

(get-coins (list 9) 6)
$10 = (+inf.0)

Answer 3

If you read the question carefully, all you need to keep track of is the number of coins needed to reach the target amount. You don't have generate every possible combination of coins to reach the target, just the one that minimizes the number of coins. And you don't even have to remember what that particular combination is, just its length. This simplifies things a bit since there's no need to build any lists.

For each denomination of coin that can possibly be used to reach the goal (So no coins bigger than the difference between the goal and the current sum), get the counts for using one of them and for using none of them, and return the minimum (Or -1 if no options present themselves).

(define (get-coins coins target)
  (calculate-coins coins 0 0 target))

;; Do all the work in a helper function
(define (calculate-coins coins coin-count amount target)
  (cond
   ((= amount target) coin-count) ; Success
   ((null? coins) -1) ; Failure
   ((> (car coins) (- target amount)) ; Current coin denomination is too big; skip it
    (calculate-coins (cdr coins) coin-count amount target))
   (else
    ;; Cases to consider:
    ;;  Adding one of the current coin to the total and leaving open using more
    ;;  Not using any of the current coins
    (let ((with-first
           (calculate-coins coins (+ coin-count 1) (+ amount (car coins)) target))
           (without-first
            (calculate-coins (cdr coins) coin-count amount target)))
      (cond
       ((= with-first -1) without-first)
       ((= without-first -1) with-first)
       (else (min with-first without-first)))))))

If you do want to get every possible combination of coin, one way is to, for each list of combinations that use a given coin, use append to combine it with a list of previous ways:

(use-modules (srfi srfi-1))
(define (get-coins2 coins target)
  (define (helper target) ; This time define a nested helper function
    (fold
     (lambda (coin ways)
       (cond
        ((= coin target) (cons (list coin) ways))
        ((< coin target)
         (append
          (map (lambda (c) (cons coin c))
               (helper (- target coin)))
          ways))
        (else ways)))
     '()
     coins))
  (let* ((ways (helper target))
         (table (make-hash-table (length ways))))
    ;; Store each combination as a key in a hash table to remove duplicates
    (for-each (lambda (way) (hash-set! table (sort-list way <) #t)) ways)
    (hash-map->list (lambda (k v) k) table)))

Examples:

scheme@(guile-user)> (load "coins.scm")
scheme@(guile-user)> (get-coins '(2) 6)
$1 = 3
scheme@(guile-user)> (get-coins2 '(2) 6)
$2 = ((2 2 2))
scheme@(guile-user)> (get-coins '(2 3) 6)
$3 = 2
scheme@(guile-user)> (get-coins2 '(2 3) 6)
$4 = ((2 2 2) (3 3))
scheme@(guile-user)> (get-coins '(9) 6)
$5 = -1
scheme@(guile-user)> (get-coins2 '(9) 6)
$6 = ()
scheme@(guile-user)> (get-coins2 '(2 3) 12)
$7 = ((3 3 3 3) (2 2 2 3 3) (2 2 2 2 2 2))
scheme@(guile-user)> (get-coins '(5 2 3 4) 21)
$8 = 5
scheme@(guile-user)> (get-coins2 '(5 2 3 4) 21)
$9 = ((2 2 2 5 5 5) (2 3 3 4 4 5) (2 4 5 5 5) (3 3 3 4 4 4) (2 2 3 4 5 5) (4 4 4 4 5) (2 2 4 4 4 5) (2 2 3 3 3 4 4) (2 2 2 2 2 3 4 4) (2 2 2 2 4 4 5) (3 3 3 3 4 5) (2 2 2 2 3 3 3 4) (2 2 2 2 2 2 2 3 4) (2 2 2 2 2 2 4 5) (3 3 3 3 3 3 3) (2 2 3 3 3 3 5) (2 2 2 2 2 2 3 3 3) (2 2 2 2 2 3 3 5) (3 3 5 5 5) (2 2 2 2 2 2 2 2 2 3) (2 2 2 2 3 5 5) (2 2 2 2 2 2 2 2 5) (2 3 4 4 4 4) (2 2 2 3 4 4 4) (2 3 3 3 3 3 4) (2 2 2 3 3 4 5) (2 2 2 3 3 3 3 3) (2 3 3 3 5 5) (3 4 4 5 5))
scheme@(guile-user)> (filter (lambda (way) (= (length way) 5)) (get-coins2 '(5 2 3 4) 21))
$10 = ((2 4 5 5 5) (4 4 4 4 5) (3 3 5 5 5) (3 4 4 5 5))

Answer 4

There are many ways to do it, here is a brute-force solution. It is not elegant but it is simple.

(define mk/pairs
  (lambda (sum coin/list)
    ((lambda (s) (s s
               (map (lambda (x) (iota (+ 1 (quotient sum x)))) coin/list)
               (lambda (s) s) ))
     (lambda (s l* ret)
       (if (null? l*)
           (ret '(()))
           (s s (cdr l*)
              (lambda (r)
                (ret (apply
                      append
                      (map (lambda (x) (map (lambda (y) (cons y x)) (car l*)))
                       r))))))))))

(define cost
  (lambda (s pair coin/list)
    (let ((sum (apply + (map * pair coin/list))))
      (and (= s sum) pair))))

(define solve
  (lambda (sum coin/list)
    (let ((pairs (mk/pairs sum coin/list)))
      (let ((solutions
             (sort (filter (lambda (x) x)
                           (map (lambda (p) (cost sum p coin/list)) pairs))
                   (lambda (p1 p2)
                     (< (apply + p1)
                        (apply + p2))))))
        (if (null? solutions)
            "fail"
            (car solutions))))))

A test looks like so:

% mit-scheme < coins.scm
MIT/GNU Scheme running under GNU/Linux

1 ]=> (solve 8 '(2 3 1))
;Value: (1 2 0)

1 ]=> (solve 6 '(2 3))
;Value: (0 2)

meaning that you have 1 coin of 2 and 2 coins of 3 in the first example and 2 coins of 3 in the second example.

I have used standard R6RS, so you should be able to convert it directly from mit/scheme to guile.